ANSWER:
C. There are two transformations: 1. a horizontal shift to the right of 9 units and 2. a vertical shift upward of 18 units.
Explanation:
We have the following functions:
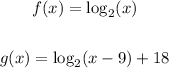
Adding or subtracting within the logarithm represents a horizontal shift, in the case of adding it moves that amount added to the left and if it subtracts it moves that amount to the right.
In this case, -9 is subtracted, which means that it moves 9 units to the right.
While if it is added or subtracted to the function, it is reflected as a vertical shift, if it is added it moves that amount up and if it is subtracted it would be down
In this case 18 is added, so it moves 18 units up.
Therefore, the correct answer is C. There are two transformations: 1. a horizontal shift to the right of 9 units and 2. a vertical shift upward of 18 units.