Question

Help on math question precalculus Question states-Which is the first step?Group of answer choicesEvaluate the second equation for x = 5.Evaluate the first equation for x = -5.Evaluate the first equation for x = -1.Evaluate the second equation for x = -1.

Answer 1

For the first equation:

When x=-5

`2x+3n`
`2(-5)+3n`
`-10+3n`

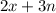
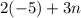
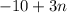
When x=-1

`2x+3n_{}`
`2(-1)+3n`
`-2+3n`

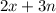
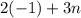
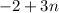
For the second equation:

When x=5

`2x^2-3x-9`
`2(5)^2-3(5)-9`
`50-15-9`
`=26`

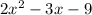
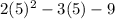
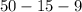
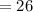
when x=-1

`2x^2-3x-9`
`2(-1)^2-3(-1)-9`
`2+3-9`
`=-4`

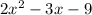
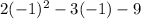
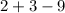
Now, we need to know the value for n to make the function continues:

We need to find when:

Lim when x tends to a of f(x)= f(-1)

Lim when x tends to -1 (negative)=-4

Lim when x tends to -1(positive) of -2+3n=-4

Solve for n :

-2+3n = -4

3n = -4+2

3n = -2

n=-2/3