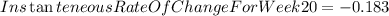Question

The following table shows the daily receipts in millions of dollars of the movie "Avatar" for successive Fridays after its opening on Friday 18 December 2009.Weeks$Receipts2 68.494 42.7856 31.288 23.61110 13.65512 6.52614 2.04716 0.84418 0.9220 0.42522 0.18824 0.07626 0.04528 0.028Estimate the instantaneous rate of change of daily receipts 20 weeks after the opening day.

Answer 1

As given from the question, we want to estimate the instanteneous rate of change of daily receipts 20 weeks after the opening day

To do this, You approximate it by using the slope of the secant line through the two closest values to your target value.

To get the instanteneous rate of change of week 20, we will be using

`\begin{gathered} week22=0.188 \\ week18=0.92 \end{gathered}`

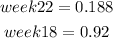
Thus,

`\begin{gathered} Ins\tan teneousRateOfChangeForWeek20=(week22-week18)/(22-18) \\ Ins\tan teneousRateOfChangeForWeek20=(0.188-0.92)/(22-18) \\ Ins\tan teneousRateOfChangeForWeek20=(-0.732)/(4) \\ Ins\tan teneousRateOfChangeForWeek20=-0.183 \end{gathered}`

The answer is

`Ins\tan teneousRateOfChangeForWeek20=-0.183`