Question

A vending machine dispenses coffee into a twelve-ounce cup. The amount of coffee dispensed into the cup is normally distributed with a standard deviation of 0.02 ounce. You can allow the cup to overfill 3% of the time. What amount should you set as the mean amount of coffee to be dispensed?

Answer 1

`11.96`

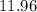
Step-by-step explanation

Parameters given:

x = 12 oz

σ = 0.02 oz

We want to find the mean amount of coffee to be dispensed if you can allow the cup to overfill 3% (0.03) of the time.

To do this, we have to first find the z value that is equal to the 97th percentile (0.97) due to the reason that everything above 12 oz will occur only 3% of the time.

To find the z value, we check the standard normal table.

The z value corresponding to 0.97 is 1.88.

Now, we can solve for the mean using the formula for z-score:

`z=(x-\mu)/(\sigma)`

where μ = mean

Therefore, the mean is:

`\begin{gathered} 1.88=(12-\mu)/(0.02) \\ \Rightarrow1.88\cdot0.02=12-\mu \\ \Rightarrow\mu=12-0.0376 \\ \mu=11.96 \end{gathered}`

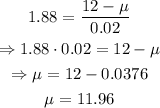
That is the answer.