The solution set are x = 8 or x= 2:
x= (8,2)
Step-by-step explanation:
The given equation:

To solve the equation using the square root property, the first thing we will do is isolate the x^2 part.
From our equation, this is already isolated as the expression with the square sign is on one side while the constant (9) is on the other side of the equation.
Next thing we will do is square root both sides of the equation:
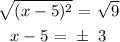
Then we will collect like terms:
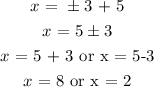
Hence, the solution set are x = 8 or x= 2
x =8, 2