Question

Pls help answer all parts. Ask if you nned a better picture of the graph please

Answer 1

In this problem, we have the following equation:

`\hat{y}=P(x)=38,257-0.1629\cdot x.`

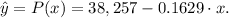
$$\hat{y}=P(x)=38,257-0.1629\cdot x.$$Where:

• y^ = P(x) = Price of x miles driven by a Ford F-150's,

,

• x = # of miles driven by a Ford F-150's.

a) For x = 100,000, we get:

`P(100,000)=21,967.`

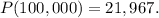
b) The general equation of a line is:

`y=b+m\cdot x\text{.}`

Where:

• b = y-intercept,

,

• m = slope.

Comparing the general equation with the equation of the problem, we have:

`m=-0.1629.`

Because the dependent and the independent variables are:

• y = Price of x miles driven by a Ford F-150's,

,

• x = # of miles driven by a Ford F-150's.

The slope m with its units is:

`m=-0.1629\cdot\frac{\text{units of price}}{\text{miles driven}}\text{.}`

c) Comparing the equation of the problem and the general equation of a line, we find the value of the y-intercept:

`b=38,257.`

The value of the y-intercept is the value of y when we have x = 0, i.e. when we have driven 0 miles. The units of the y-intercept are the same as the variable y, so the y-intercept with units is:

`b=38,257\text{ units of price.}`

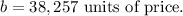
d) Replacing the value x = 58,000 in the equation of the line, we get:

`\hat{y}=38,257-0.1629\cdot58,000=28,808.8.`

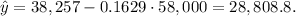
The residual is the difference between the y coordinate of the point (58,000, $30,000) and the value of y^ that we have computed:

`\text{Residual = }y-\hat{y}=30,000-28,808.8=1,191.2`

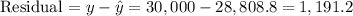
Answers

a) The price for 100,000 driven is $21,967.

b) The slope of the line is the price per unit of a mile driven:

`m=-0.1629\cdot\frac{\text{units of price}}{\text{miles driven}}\text{.}`

c) The y-intercept of the line is the cost of when the number of miles driven is zero:

`b=38,257\text{ units of price.}`

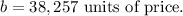
d) Residual = $1,191.2.