The Properties of Logarithms are shown below:
• a)
To rewrite the first logarithm, we have to remember that:
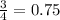
Therefore, we can rewrite the expression as follows:
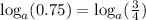
Using the property of division of the logarithms we get:

Replacing the given values:
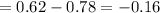
• b)
Also, if we multiply 3 times 4 we get 12. Thus, we can rewrite the second expression:
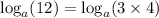
Using the multiplication property of the logarithm:
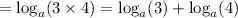
Replacing the values:
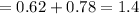
• c)
Finally, for the last expression we have to remember that a square root can also be written as an exponent:
![\log _a(\sqrt[]{3})=\log _a(3^{(1)/(2)})](https://img.qammunity.org/2023/formulas/mathematics/high-school/cragrls1gq39s89oy3zudkqlj5e3ldgvy4.png)
Then, using the exponentiation property of the logarithms we can rewrite that last expression:
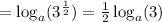
As we already know the value of loga(3), we can just replace it and get the result:
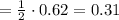
Answer:
• a) -0.16
,
• b) 1.4
,
• c) 0.31