Question

Im having hard problems with (function A) y=-3x+2 (Function B) X=0,2,4,6 Y=2,1,0,-1

Answer 1

First, we find the equation of the function B:

The equation is of the form y = mx + b, where m is:

`m=(y2-y1)/(x2-x1)`

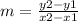
We have the points P1(0,2) and P2(4,0), so

`m=(0-2)/(4-0)=-(2)/(4)=-(1)/(2)`

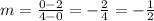
And b is:

`\begin{gathered} y=mx+b \\ \text{we use the point (0,2)} \\ 2=-(1)/(2)(0)+b \\ b=2 \end{gathered}`

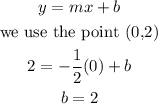
Therefore, the function B is:

`y=-(1)/(2)x+2`

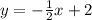
Next, we solve the system of equations:

`\begin{gathered} y=-3x+2 \\ y=-(1)/(2)x+2 \end{gathered}`

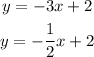
Substitute y:

`-3x+2=-(1)/(2)x+2`

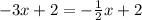
Solve for x:

`\begin{gathered} -3x+(1)/(2)x+2=-(1)/(2)x+(1)/(2)x+2 \\ -(5)/(2)x+2=2 \\ -(5)/(2)x+2-2=2-2 \\ -(5)/(2)x=0 \\ x=0 \end{gathered}`

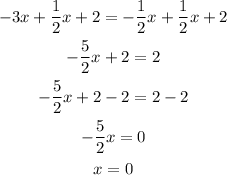
Then for y:

`y=-3(0)+2=0+2=2`

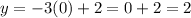
Answer:

x = 0

y = 2