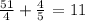To solve the equation
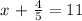
First, subtract 4/5 to both sides of the equation, and then make the corresponding operations:
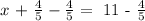
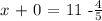
We can solve 11 - (4/5) multiplying the denominator 5 by 11, and then the denominator of 11, which is 1, by -4. Then divide the numerator by the multiplication of both denominators (1 * 5= 5).
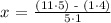
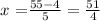
To check, we have: