Answer
There are C(20, 5) = 15504 ways to select 5 extras out of a group of 20 people
Explanation
A combination is a grouping of outcomes in which the order does not matter (A and then B is the same pair as B and then A).
The number of combinations of n things chosen k at a time is found using:
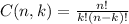
In this case, the director has to select k = 5 extras out of a group of n = 20 people, that is,
![C(20,5)=(20!)/(5!(20-5)!)=(20!)/(5!15!)=\frac{20\cdot19\cdot18\operatorname{\cdot}17\operatorname{\cdot}16\operatorname{\cdot}15!}{120\cdot15!}=\frac{20\cdot19\cdot18\operatorname{\cdot}17\operatorname{\cdot}16}{120}=15504]()