Question

-%deviation from expected value (show calculations) for the relation between Fc and f^2.

Answer 1

In the given experimental setting we are asked to determine the relationship between the centripetal force and the frequency. To do that we will use the following formula that relates the centripetal force and the square of the frequency:

`F_c=4\pi^2m_srf^2`

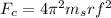
Where:

`\begin{gathered} F_c=\text{ centripetal force} \\ m_s=\text{ mass of the rubber stopper} \\ r=\text{ radius} \\ f^=\text{ frequency} \end{gathered}`

First, we divide both sides by the square of the frequency:

`(F_c)/(f^2)=4\pi^2m_sr`

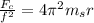
Now, we substitute the values of the stopper mass and the radius:

`(F_c)/(f^2)=4\pi^2(0.0153kg)(0.265m)`

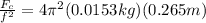
Solving the operations:

`(F_c)/(f^2)=0.16kg*m`

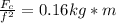
Therefore, for a fixed rubber mass and a fixed radius, the quotient of the centripetal force and the square of the frequency is always 0.16 theoretically.

Now, we will determine the quotient between the centripetal force and the square of the frequency with the experimental data.

First, the centripetal force is equivalent to the weight of the hanging mass since the tension is the chord is the same, therefore, we have:

`F_c=m_hg`

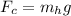
Where:

`m_h=\text{ hanging mass}`

Now, the frequency is equivalent to the number of cycles per unit of time, therefore, the frequency is:

`f=\frac{revolutions\text{ }}{time}`

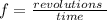
For the 20g mass and trial 1 we have the following values:

`\begin{gathered} m_h=20g=0.02kg \\ revolutions\text{ =}26 \\ time\text{ =}10s \end{gathered}`

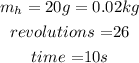
Substituting the values we get:

`(F_c)/(f^(^2))=(m_hg)/(((revolutions)/(time))^2)=((0.02kg)(9.8(m)/(s^2)))/(((26rev)/(10s))^2)`

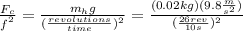
Solving the operations:

`(F_c)/(f^2)=0.03kg*m`

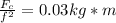
Now, we determine the deviation from the theoretical value using the following formula:

`D=(E.value-T.value)/(T.value)*100`

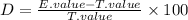
Substituting we get:

`D=(0.03-0.16)/(0.16)*100=-81.25\%`

The same procedure is used for the other trials.