Question

PRE CALC SUBJECT.I need this practice problem answeredI will provide another pic with the answer options

Answer 1

The general equation of the ellipse is as follows:

`((x-h)^2)/(b^2)+((y-k)^2)/(a^2)=1`

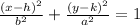
where (h, k) is the center of the ellipse.

Thus, the center of the given ellipse is (6,-3).

The endpoints of the major axis is given by the following expression:

`(h,k\pm a)`

From the given equation, the value of a² is 100. Thus, the value of a is 10.

Substitute the value of h, k, and a into the coordinates of the endpoints of the major axis.

`(h,k\pm a)=(6,-3\pm10)`

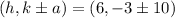
Thus, the endpoints of the major axis are (6,7) and (6,-13).

This means that the endpoints of the major axis is 10 units away from the center.

On the other hand, the endpoints of the minor axis is b units away from the center. The value of b can be obtained from the equation.

Since b² is 36, the value of b must be 6. Thus, the endpoints of the minor axis is 6 units away from the center.

To graph the ellipse, the endpoints of the minor and major axes must be connected with a smooth curve.

To obtain the endpoints of the minor axis, substitute h, k, and b into the following coordinates.

`(h\pm b,k)=(6\pm6,-3)`

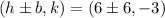
Thus, the endpoints of the minor axes are (0,-3) and (12,-3).

Finally, to graph the ellipse, draw a smooth curve passing through the endpoints of the major and minor axes: (6,7), (6,-13), (0,-3) and (12,-3).