The volume of recangular prism can be calculated as:

V: volume
w: width
l: length
h: height
The box heigth has been increased by 15%, this means that to the original heigth 0.15% of it has been added:
Let "x" represent the original height of the box
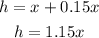
The box length has been increased by 25%, this means that to the original length, 0.25 more has been added
Let "y" represent the length of the box:
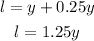
Let "z" represent the original width of the box.
The original volume of the box can be calculated as:

And the new volume of the box can be calculated as
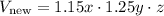
To calculate the percentage increase you have to subtract the old volume from the new one and divide it by the old volume.
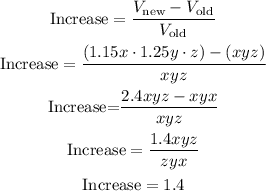
The 1 represents the original volume, so that the box volume was increased 0.4 of its original volume.
Multiply it by 100 and the percentaje is 40%