Hello there. To solve this question, we'll have to remember some properties about finding the common denominator in a sum of fractions.
Given the equation:

We have to determine its least common denominator.
For this, remember the definition for least common factor of polynomials:
If f(x) and g(x) are polynomials, their lcm(f(x), g(x)) can be calculated as:

Where gcd(f(x),g(x)) is the greatest common divisor of the polynomials.
Usually, this expression gives another polynomial, as you can see we're dividing the product between f and g by their gcd.
In this case, notice f and g are linear functions. Most specifically they're first degree polynomials with leading coefficient equal 1 (monoic).
In this case, if f(x) is not equal to g(x), then we show that

Such that their lcm is simply given by
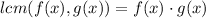
Therefore we have the least common denominator of this equation as
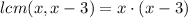
This is the answer contained in the option b).