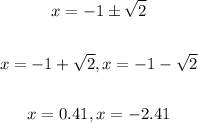Question

Solve the quadratic equation by completing the squarex^2+2x-1=0First, choose appropriate form and fill in the blanks with the correct numbers. Then, solve the equation. Around your answer to the nearest hundredth. If there is more than one solution, separate them with commas.

Answer 1

Given the equation;

`x^2+2x-1=0`

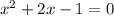
Using completing the square method; take one to the other side of the equation and change the sign.

`x^2+2x=1`

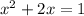
Add the square of half of the coefficient of x to both sides of the equation;

`\begin{gathered} x^2+2x+((1)/(2)(2))^2=1+((1)/(2)(2))^2 \\ \\ x^2+2x+1=1+1 \end{gathered}`

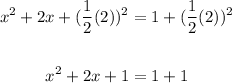
Factorize the left side and simplify the right side;

`(x+1)^2=2`

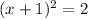
Thus, the form is;

`(x+1)^(2)=2`

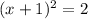
And the solution is;

`\begin{gathered} x=-1\pm√(2) \\ \\ x=-1+√(2),x=-1-√(2) \\ \\ x=0.41,x=-2.41 \end{gathered}`