Question

What is the difference in cubic centimeters between in a large scoop of ice cream and a small scoop of ice cream? Round Your Answer To The Nearest Tenth.

Answer 1

Step-by-step explanation:

We first need to calculate the volume of each scoop of ice cream. So, the volume of a sphere can be calculated as:

`V=(4)/(3)\cdot\pi\cdot r^3`

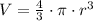
Where r is the radius of the sphere.

Then, if the diameter of the small scoop is 8 cm, the radius is 4 cm because the radius is half the diameter. So, the volume of the small scoop of ice cream is:

`\begin{gathered} V=(4)/(3)\cdot3.14\cdot4^3 \\ V=(4)/(3)\cdot3.14\cdot64 \\ V=267.95cm^3 \end{gathered}`

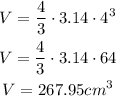
In the same way, if the diameter of the large scoop is 12 cm, the radius is 6 cm, so the volume is:

`\begin{gathered} V=(4)/(3)\cdot3.14\cdot12^3 \\ V=(4)/(3)\cdot3.14\cdot1728 \\ V=7234.56cm^3 \end{gathered}`

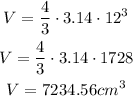
Finally, the difference between the large and small scoop of ice cream is:

Difference = 7234.56 cm³ - 267.95 cm³

Difference = 6966.61 cm³

Therefore, the answer is 6966.61 cm³