We can use the following equation to describe the exponential function:
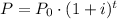
Where P is the final value after t years, P0 is the initial value and i is the growth rate per year.
Using P0 = 15 and i = 6.4% = 0.064, we have:
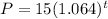
Now let's check each option:
A) For t = 12 we have:
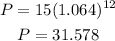
The population is approximately 31,578, so this option is incorrect.
B) For t = 15 we have:
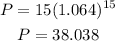
This option is also incorrect, the population is under 40,000.
C) For t = 18:
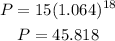
The population is under 50,000, so this option is correct.
D) For t = 20:
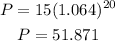
The population is not over 300,000, so this option is incorrect.
The correct option is C.