Question

Help Solving Angle X is a right angle Angle X is 51 degrees Side XZ is 10 Centimeters Side XY is a Hypotenuse Calculate the lengths of side XY and YZ

Answer 1

So we need to find side XY and YZ. For this purpose we can use the tangent. The tangent of an angle is given by:

`\tan \alpha=\frac{\text{ opposite sides}}{\text{ adjacent sides}}`

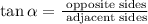
The opposite side of angle X is YZ and the adjacent is XZ=10 then its tangent is equal to:

`\begin{gathered} \tan X=(YZ)/(XZ) \\ \tan 51^(\circ)=(YZ)/(10) \\ 1.235=(YZ)/(10) \end{gathered}`

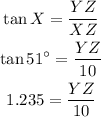
Then if we multiply both sides by 10 we can find the measure of YZ:

`\begin{gathered} 1.235=(YZ)/(10) \\ 10\cdot1.235=(YZ)/(10)\cdot10 \\ 12.35=YZ \end{gathered}`

So we found the length of YZ. In order to find XY we can use the Pythagorean theorem. For this triangle this theorem states:

`XY=\sqrt[]{XZ^2+YZ^2}`

We replace XZ and YZ with the lengths we found and we get:

`\begin{gathered} XY=\sqrt[]{XZ^2+YZ^2} \\ XY=\sqrt[]{10^2+12.35^2}=\sqrt[]{252.5225} \\ XY=15.89 \end{gathered}`

Then the length of XY is 15.89cm and the length of YZ is 12.35cm.