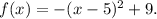Since the function increases when x goes from -∞ to 5, and decreases when x goes from 5 to ∞, then the parabola has a maximum at its vertex, therefore it is a concave down parabola.
The general form of a concave down parabola, with vertex (5,9) is:
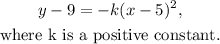
Answer: Option d)