We first verify that the equation is balanced. We have 5 carbons (C), 2 sulfurs (S), and 4 oxygens (O) on each side of the reaction. So the reaction is balanced.
a) Now if we look at the reaction we can see that when 2 moles of SO2 react, 1 mole of CS2 is produced. That is, the ratio is 2 to 1. For each mole of SO2 half as many moles of CS2 will be produced.
So if we have 9.5 moles of SO2 we will have 9.5/2 moles, that is 4.75 moles of CS2.
Answer a) By reacting 9.50 moles of SO2 with an excess of it would be produced 4.75 moles of CS2.
Now, for the following parts of the question, we can apply the ideal gas law. This is because the reaction is in the gas phase and the law applies only to gases.
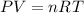
Where,
P= Pressure at STP = 1 atm
T= Temperature at STP = 273.15K
R= Ideal law constant = 0.08206 (atm L)/(mol K)
V= Volume of the gas
n= Numer of moles
b)We clear n and we replace the known values of SO2 to find the number of moles of SO2 that react.
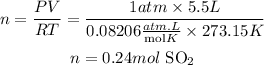
Now, for each mole of SO2 that reacts we need 5/2 moles of C, that is 0.24x5/2=0.61 moles of C.
We use mass molar of C to calculate the grams.
Mass molar of C=12.01g/mol
Mass of C= Moles of C x Mass Molar
Mass of C= 0.61 mol x 12.01 g/mol = 7.37 g
So, To fully react 5.5 L of SO2 at STP we will need 7.37 g of C.
c)We apply the gas law again but this time we clear the volume.
We also take into account that for each mole of C, 4 moles of CO are produced, so if we have 20 moles of C we will produce 20x4=80 moles of CO.
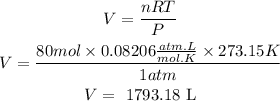
So, from 20.0 moles of C at STP can be produced 1793.18 liters of CO