Question

face individually based on the provided information. Use this information to answer each of questions that follow. a. A sporting goods manufacturer, AC Sports, wants to produce a basketball with a diameter of 9 inches for younger players. Exactly how much material would be needed for each basketball? Type your response here: b. The same manufacturer plans to package the ball along with some other gear kids can use to get started playing basketball. The box that will hold everything will be 10 inches long, 12 inches wide, and 10 inches tall. The packaging department needs to know how many square inches of cardboard will be needed to create each box. how much will it need per box?type your responses here:

Answer 1

The basketball is a sphere of radius(r) 4.5 inches.

`r=(diameter)/(2)=(9)/(2)=4.5\text{ inches}`

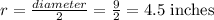
By formula,

Area of a Sphere is given below:

`\begin{gathered} A=4\pi r^2 \\ \text{Where A =area ; r=radius=4.5 inches} \\ \text{Substituting these values in the formula above, we get} \\ A=4*(22)/(7)*(4.5)^2=254.571\text{ }\approx\text{ 254.57 square inches} \end{gathered}`

The exact material needed for each basketball is 254.57 square inches

b. The surface area of each box is a cuboid.

The surface Area of a cuboid is given by the formula below:

`\begin{gathered} SA=2(lb+lh+bh) \\ \text{Where l=10 inches ; b=12 inches ; and h=10 inches ; SA = surface area} \\ SA=2\lbrack(10*12)\text{ +(10}*10)+(12*10)\rbrack \\ SA=2(120+100+120) \\ SA=2*340=680\text{ square inches} \end{gathered}`

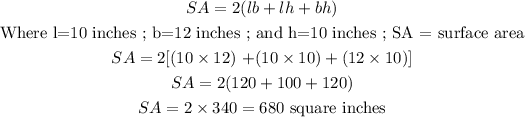
Thus, the square inches of cardboard needed for each box is 680 square inches.