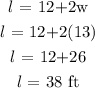Question

The length of a rectangle is 12 ft longer than twice the width. If the perimeter is 102 ft, find the length and width of the rectangle

Answer 1

Answer;

`\begin{gathered} \text{Length = 38 ft} \\ \text{Width = 13 ft} \end{gathered}`

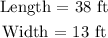
Explanation;

Here, we want to get the length and width of the rectangle

Let the length of the rectangle be x ft

Let the width of the rectangle be w ft

From the question, the length is 12 ft more than twice the width

We have this as;

`l\text{ = 12 + 2w}`

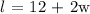
Mathematically, the formula for the perimeter of a rectangle is;

`P\text{ = 2(l+w)}`

Now, substitute the value for l above and perimeter from the question

We have that as;

`\begin{gathered} 102\text{ = 2(12+2w+w)} \\ 51\text{ = 12 + 3w} \\ 3w\text{ = 51-12} \\ 3w\text{ = 39} \\ w\text{ = }(39)/(3) \\ w\text{ = 13 ft} \end{gathered}`

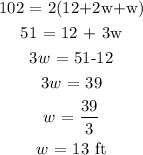
Recall;

`\begin{gathered} l\text{ = 12+2w} \\ l\text{ = 12+2(13)} \\ l\text{ = 12+26} \\ l\text{ = 38 ft} \end{gathered}`