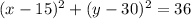You know that the length and the width of the rectangular backyards are:
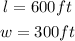
Knowing the coordinates of the vertices of the rectangle, you can plot them on a Coordinate Plane and draw the rectangle. Notice that the vertices are:
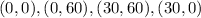
See the picture below:
According to the information given in the exercise, a circular flower garden is dug to be exactly in the center of the backyard. The radius of this circle is:
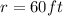
If you draw the diagonals of the rectangle, you can find its center and therefore, the center of the circle. See the picture below:
Now you know the center of the circle.
By definition, the equation of a circle is:
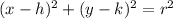
Where "r" is the radius of the circle and its center is:
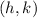
Since you already know the center of the circular flower garden and its radius, you only need to substitute values into the equation and simplify:
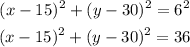
Therefore, the answer is: