Question

Q7. A is the point with coordinates (5,9)B is the point with coordinates (d, 15)The gradient of the line AB is 3Work out the value of d.

Answer 1

We solve as follows:

*First: We find the area of the trapezium:

`A=(a+b)/(2)h`

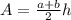
Here a & b are the bases and h is the height, now we replace:

`A=(16+10)/(2)\cdot7.6\Rightarrow A=98.8`

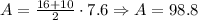
So, the area of the trapezium is 98.8 squared meters.

We know that 1 liter covers 1.9 squared meters, now we determine how many liters of paint we will need:

`p=(1\cdot98.8)/(1.9)\Rightarrow p=52`

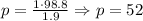
So, we will need 52 liters of paint, now we will determine the cost:

Since we will need more than 50 liters, then we take it to 55 liters in total (Since the tin of paint is sold for 5 liters each) and calculate the cost:

`x=(55\cdot16.99)/(5)\Rightarrow x=(18689)/(100)\Rightarrow x=186.89`

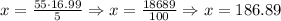
So, it will cost £186.89 to buy the paint.