Let x be the unknown number. Then, the statement "8 increased by three times a number" can be written as

and the statement "it is a least 4 more than the number" can be written as
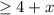
By combining these result, the inequality is:
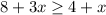
Now, let's solve for x.
By subtracting x to both sides of the last inequality, we get

and by subtracting 8 to both sides, we have
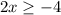
By dividing both sides by 2, we obtain
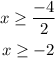
Therefore, the solution is:
