Question

Find the area of the sector of the circle with central angle of 205° and radius of 7 cm. Use 3.14 for pi(π) and round to the nearest hundredth.Group of answer choices25.03 cm243.80 cm276.97 cm287.61 cm2

Answer 1

87.61 cm²

Explanation:

The area of a sector is calculated using the formula:

`A=(\theta)/(360)*\pi r^2`

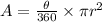
Given:

• The central angle,θ = 205°

,

• The radius of the circle, r = 7cm

,

• π = 3.14

Substitute these values into the formula:

`\begin{gathered} A=(205)/(360)*3.14*7^2 \\ \approx87.61\;cm^2 \end{gathered}`

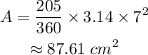
The area of the sector is 87.61 cm² (rounded to the nearest hundredth).