Question

Complete the table of the two function and then select the value that is a solution to f(x) = g(x)

Answer 1

`x=5`

Step-by-step explanation

We want to fill the table with the values of the given functions:

`\begin{gathered} f(x)=-x^2+4x+12 \\ \\ g(x)=x+2 \end{gathered}`

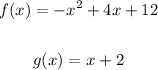
To do this, we have to substitute the values of x for each function and simplify it.

For f(x), we have that the values of the function are:

`\begin{gathered} x=1: \\ \\ f(1)=-(1)^2+4(1)+12=15 \\ \\ x=2: \\ \\ f(2)=-(2)^2+4(2)+12=16 \\ \\ x=3: \\ \\ f(3)=-(3)^2+4(3)+12=15 \\ \\ x=4: \\ \\ f(4)=-(4)^2+4(4)+12=12 \\ \\ x=5: \\ \\ f(5)=-(5)^2+4(5)+12=7 \\ \\ x=6: \\ \\ f(6)=-(6)^2+4(6)+12=0 \end{gathered}`

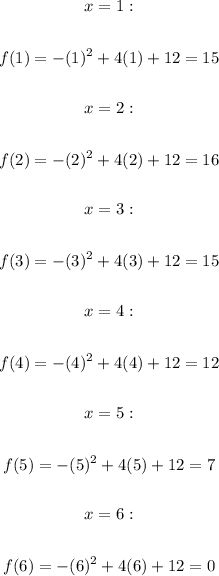
For g(x), we have that the values of the function are:

`\begin{gathered} x=1: \\ \\ g(1)=1+2=3 \\ \\ x=2: \\ \\ g(2)=2+2=4 \\ \\ x=3: \\ \\ g(3)=3+2=5 \\ \\ x=4: \\ \\ g(4)=4+2=6 \\ \\ x=5: \\ \\ g(5)=5+2=7 \\ \\ x=6: \\ \\ g(6)=6+2=8 \end{gathered}`

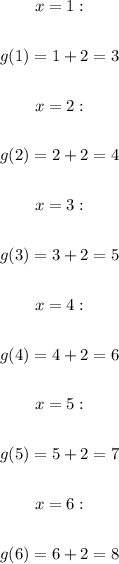
Now, let us fill the table:

We want to select the value of x such that the two functions are equal. To do this, locate the value of x on the table where both f(x) and g(x) have the same value.

From the table, we have that the value of x for which f(x) = g(x) is:

`x=5`