Answer:
Step-by-step explanation:
Given:
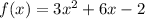
There are ways to find the minimum value of the given function. We graph it or express it into vertex form:
For the graph:
Based on the graph, the lowest point is at (-1,-5).
We can double check this by expressing it into vertex form:
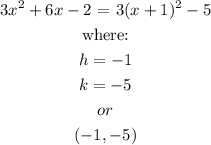
Therefore, the minimum value is (-1,-5)