1 Answer

Jviotti · Answer 1 · 2023-03-19T22:24:32+0000

Let us solve the part d.

The given sequence is

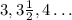
$3,3(1)/(2),4\ldots$

Please note that 3 and a half is basically 3.5

The standard explicit formula for an arithmetic sequence is given by

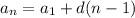
$a_n=a_1+d\mleft(n-1\mright)$

Where aₙ is the nth term, a₁ is the first term and d is the common difference

The common difference is basically the difference between any two consecutive terms

d = 4 - 3.5 = 0.5

d = 3.5 - 3 = 0.5

So the common difference is 0.5

The first term in the sequence is 3

So the explicit formula for an arithmetic sequence becomes

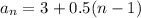
$a_n=3_{}+0.5(n-1)$

Now to find the 16th term we will simply substitute n = 16 in the above formula.

$\begin{gathered} a_(16)=3_{}+0.5(16-1) \\ a_(16)=3_{}+0.5(15) \\ a_(16)=3_{}+7.5 \\ a_(16)=10.5 \end{gathered}$

Therefore, the 16th term of the sequence is 10.5.

Please log in or register to add a comment.