Answer:
a) Horizontal component of its initial velocity = 34.4 m/s
b) Vertical component of its initial velocity = 24.09 m/s
c) The maximum height attained by the arrow = 29.6 m
d) Time taken to reach the maximum height = 2.458 s
e) Total amount of time spent in the air = 4.916 seconds
f) The arrow strikes the ground after travelling an horizontal distance of 169.11 m
g) Horizontal component of its velocity just prior to impact = 34.4 m/s
h) Vertical component of its velocity just prior to impact = -24.09 m/s
i) The magnitude of its velocity just prior to impact = 42 m/s
j) The direction of its velocity just prior to impact = 35°
Step-by-step explanation:
Initial velocity, u = 42 m/s
Angle, θ = 35°
a) Horizontal component of its initial velocity
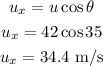
Horizontal component of its initial velocity = 34.4 m/s
b) Vertical component of its initial velocity
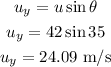
Vertical component of its initial velocity = 24.09 m/s
c) Maximum height attained by the arrow
Note that when the arrow goes up, it will surely come down. It will reach the maximum height at a time that is half of the total time that it will spend in the air
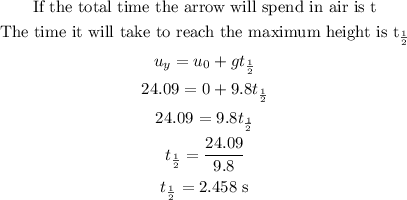
Maximum height attained by the arrow is calculated below
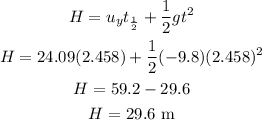
The maximum height attained by the arrow = 29.6 m
d) Time taken to reach the maximum height = 2.458 s (As calculated above)
e) Total amount of time spent in the air
The total amount of time spent in the air = Time taken to reach the maximum height + Time taken to fall back to the ground
t = 2.458 s + 2.458 s
t = 4.916 s
Total amount of time spent in the air = 4.916 seconds
f) How far away does it strike the ground?
This will be the horizontal distance travelled by the arrow. Therefore, the horizontal component of the velocity will be used
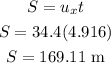
The arrow strikes the ground after travelling an horizontal distance of 169.11 m
g) Horizontal component of its velocity just prior to impact
The horizontal component of the velocity prior to impact will still remain as 34.4 m/s
h) Vertical component of its velocity just prior to impact
This will be in opposite to the initial velocity when the arrow was fired
Therefore, the vertical component of its velocity just prior to impact = -24.09 m/s
i) The magnitude of its velocity just prior to impact
![\begin{gathered} v^2=u^2_x+u^2_y \\ v^2=34.4^2+(-24.09)^2 \\ v=\sqrt[]{34.4^2+(-24.09)^2} \\ v=42\text{ m/s} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/o3yvbw91rh3zfg3gffho7dwikxarwclaec.png)
The magnitude of its velocity just prior to impact = 42 m/s
j) The direction of its velocity just prior to impact
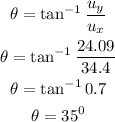
The direction of its velocity just prior to impact = 35°