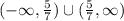Given the function
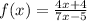
The inverse is given by
Replace f(x) with y:
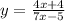
Swap x with y:
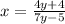
Solve for y:
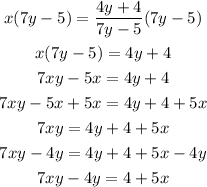
Factor
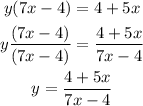
Answer:
the inverse of function f is, replace y with f^-1(x)
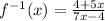
Domain of f^-1
These are the x-values of the function. First, Find undefined points
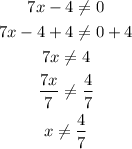
We have that x must be different from 4/7 therefore the domain is:
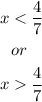
Answer:
in interval notation
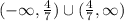
Range of f^-1
These are the values and for which the function is defined. In this case, we have that given a function f and its inverse the domain of f becomes the range of f^-1. Therefore, we find the domain of the function f:
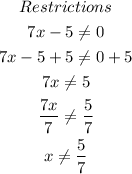
We have that x must be different from 5/7, so:
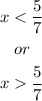
Combining the ranges
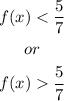
Answer:
the range in interval notation