Question

When 100 = 5 + 2) is solved for c, one equation is c = (26-2)2 Which of the following is an equivalent equation to findc?O C-100-10-5O C= (100-10-5)2(106-22O C-25oC(106-101225

Answer 1

Given: The formula below

`10b=5(\sqrt[]{c}+2`

To Determine: The equivalent of c given that it was solved to be

`c=(2b-2)^2`

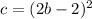
Solution

`10b=5(\sqrt[]{c}+2)`

Divide both side by 5 as below

`\begin{gathered} (10b)/(5)=\frac{5(\sqrt[]{c}+2)}{5} \\ (10b)/(5)=\sqrt[]{c}+2 \end{gathered}`

Subtract to from both sides

`\begin{gathered} (10b)/(5)-2=\sqrt[]{c}+2-2 \\ (10b)/(5)-2=\sqrt[]{c} \end{gathered}`

Make the left hand sides into a single fraction

`(10b-10)/(5)=\sqrt[]{c}`

Take squares of both sides

`\begin{gathered} ((10b-10)/(5))^2=(\sqrt[]{c})^2 \\ ((10b-10)^2)/(5^2)=c \\ ((10b-10)^2)/(25)=c \end{gathered}`

Hence,

`c=((10b-10)^2)/(25)`

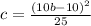
OPTION D is the correct answer