To find the solution of the given equation, substract 10m from both sides of the equation to write it in standard form:
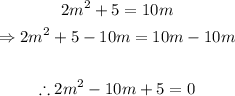
Use the quadratic formula with a=2, b=-10 and c=5 to find the solutions to this quadratic equation:
![\begin{gathered} m=\frac{10\pm\sqrt[]{(-10)^2-4(2)(5)}}{2(2)} \\ \\ \Rightarrow m=\frac{10\pm\sqrt[]{100-40}}{4} \\ \\ \Rightarrow m=\frac{10\pm\sqrt[]{60}}{4} \\ \\ \Rightarrow m=\frac{10\pm2\cdot\sqrt[]{15}}{4} \\ \\ \Rightarrow m=\frac{5\pm\sqrt[]{15}}{2} \\ \\ \therefore m_1=\frac{5+\sqrt[]{15}}{2}\approx4.436 \\ \therefore m_2=\frac{5-\sqrt[]{15}}{2}\approx0.564 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/h65f1nj3az38rug7vzif1s7h6eiihx1pm6.png)
To find five points to draw a graph of a parabola, replace the values 0, 1, 2, 4 and 5 into the expression for f(m):
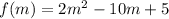
Then:
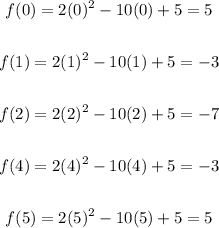
Then, five points on the graph of f(m) are (0,5), (1,-3), (2,-7), (4,-3) and (5,5).
Plot those five points and draw a parabola through them:
Notice that it is not possible to give integer roots. In this case, we can detect that there is a root between two values of m if the function f(m) changes it sign.
Notice that f(0)=5 and f(1)=-3. Then, the first root is between 0 and 1.
Notice that f(4)=-3 and f(5)=5. Then, the second root is between 4 and 5.