Answer:
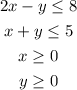
Explanation:
To determine the inequalities that represent the graph, we need to find the equations for the lines on the graph.
The line is represented by the following equation:

Therefore, if the line goes down, has a y-intercept of 5, we can calculate the slope with change in y over change in x:
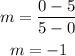
The equation of the line is:
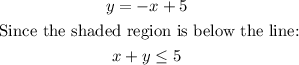
The shaded region also has limits with x=0 and y=0, then:
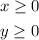
For the other line, which has a y-intercept of -8 and rate of change (slope):
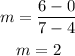
Its equation would be:
