Question

a bag contains 4 red marbles 3 blue marbles 2 yellow Marbles and 1 green marble in Marble is drawn from the bag without replacement then a second marble is drawn then what is the probability that both marbles are yellow

Answer 1

Given:

4 red marble

3 blue marble

2 yellow marble

1 green marble

Total marble = 4 + 3 + 2 + 1 = 10 marble

Probability is given by

`pr\text{ =}\frac{\text{Number of required outcome}}{Total\text{ number of sample}}`
`pr\text{ =}\frac{\text{Number of required outcome}}{Total\text{ number of sample}}\text{ =}\frac{Number\text{ of yellow}}{\text{Total number of marble}}`

`pr\text{ = }(2)/(10)`

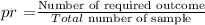
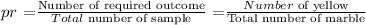
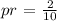
If the yellow ball is drawn again, the total number of the yellow ball will be reduced to 1, and the total number of marble is given to be 9

Then the probability will be

`pr\text{ =}(1)/(9)`

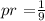
Then the probability that both are yellow are

`(2)/(10)\text{ x }(1)/(9)\text{ =}(2)/(90)\text{ =}(1)/(45)`

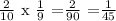
The probability that both are yellow = 1/45