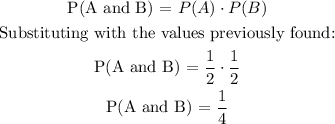Events
• A: an even number is rolled in the first time
,
• B: a number greater than 3 is rolled the second time
The probability of rolling an even number is:
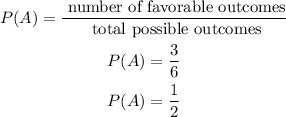
The probability of rolling a number greater than 3 is:
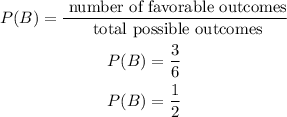
Events A and B are independent, then the probability of one happening after the other is: