We know that the height is given by the equation:
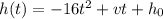
in this case the initial velocity is 72 ft/s and the inital height is 25 ft. Plugging this values the height function for the ball is:
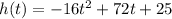
If we want to know the height after 4 seconds we evaluate the function at t=4, then we have:
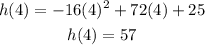
Therefore the height of the ball after four seconds is 57 ft.