Question

Hello! May I get an answer to this question if possible?

Answer 1

In the question, we are given the following parameters.

`\begin{gathered} \text{Distance covered(Upstream or downstream)=8miles} \\ \text{Time taken for the motor boat(Upstream) = 20 minutes} \\ \text{Time taken for the motor boat (Downstream) =30 minutes} \end{gathered}`

Step-by-step explanation

Using the given parameters, we will make the following assumptions.

Let x = speed of the boat,

Let y = speed of the current.

Recall,

`\text{Speed = }\frac{Dis\tan ce}{\text{Time}}`

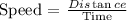
Therefore we can create a simultaneous equation below.

A motorboat can go 8 miles downstream on a river in 20 minutes or 20/60hours.

`\begin{gathered} \Rightarrow\text{speed of boat + sp}eed\text{ of current = sp}eed(downstream) \\ \Rightarrow x+y=(8)/((20)/(60)) \\ \Rightarrow x+y=24-----1 \end{gathered}`

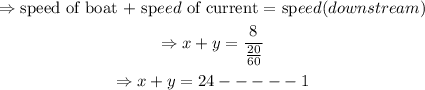
Also, A motorboat can go 8 miles upstream on a river in 30 minutes or 30/60hours.

`\begin{gathered} \Rightarrow\text{speed of boat - sp}eed\text{ of current = sp}eed(upstream) \\ \Rightarrow x-y=(8)/((30)/(60)) \\ \Rightarrow x-y=16----2 \end{gathered}`

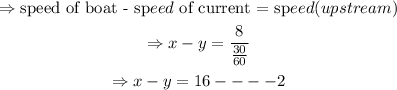
Therefore, if we subtract equation two from one we will then get the speed of the current.

`\begin{gathered} \Rightarrow x-x+y-(-y)=24-16 \\ \Rightarrow y+y=8 \\ \Rightarrow2y=8 \\ \Rightarrow y=(8)/(2) \\ \Rightarrow y=4\text{miles per hour} \end{gathered}`

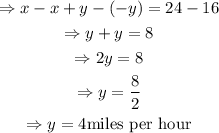
Answer: The speed of the current is 4 miles per hour