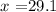1 Answer

Deduplicator · Answer 1 · 2023-06-17T01:02:50+0000

Question:

Solution:

We can apply the Law of Cosines. This law establishes the following: consider the following triangle:

then, we can find the side C by the following equation:

$c\text{ = }\sqrt[]{a^2+b^2-2ab\cos \gamma}$

in this case, we have that:

$c\text{ = x}$

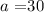
$a\text{ =30}$

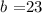
$b\text{ =}23$

and

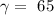
$\gamma=\text{ 65}$

Replacing these data in the equation of the law of cosines we obtain:

$x\text{ = }\sqrt[]{30^2^{}+23^2-2(30)(23)\cos (65)\text{ }}\text{ }$

this is equivalent to:

$x\text{ = }\sqrt[]{30^2^{}+23^2-2(30)(23)\cos(65)\text{ }}=\text{ 29.08 }\approx29.1$

then, the correct answer is:

$x\text{ =}29.1$

Please log in or register to add a comment.