Let's draw the problem:
As we can see, we have a pair of right triangles, and for both the distance we want if the adjacent leg with respect to the known angles. The opposite legs add up to the monument heigh.
So, we can use tangent of each angle to find the portion of the height and add them:
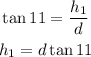
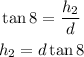
Since h1 and h2 add to 150 ft, we have:
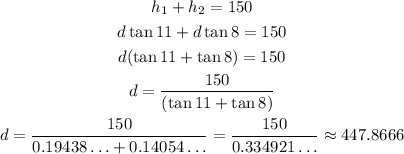
So, the distance is 447.8666 ft.