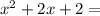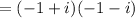Step-by-step explanation
Since we have the expression:
(x + a)^2 = b
And the quadratic expression:
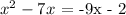
Adding +2 to both sides:
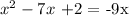
Adding +9x to both sides:
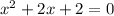
Now, rewriting the expression:
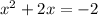
Now, completing the square of:
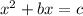
We need to add b^2/4 to both sides:
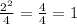
Now, we get:
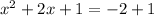
and get:
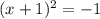
Therefore, we need to take square roots of the expression to get:
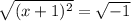
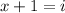
Isolating x:
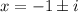
Therefore: