Question

Allison earned a score of 775 on Exam A that had a mean of 700 and a standarddeviation of 50. She is about to take Exam B that has a mean of 350 and a standarddeviation of 100. How well must Allison score on Exam B in order to do equivalentlywell as she did on Exam A? Assume that scores on each exam are normallydistributed

Answer 1

The formula for the z-score is,

`z=(x-\mu)/(\sigma)`

Determine the z-score for Exam A.

`\begin{gathered} z_A=(775-700)/(50) \\ =-(75)/(50) \\ =-1.5 \end{gathered}`

For equivalent the z score of both the exams must be equal.

Determine the value of x for z = -1.5.

`\begin{gathered} -1.5=(x-350)/(100) \\ x-350=150 \\ x=350+150 \\ =500 \end{gathered}`

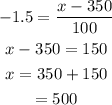
So Allison must score 500 marks in Exam B in order to do equivalently

well as she did on Exam A.