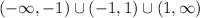Question

What is the domain of function g(x)=x+1/(x+1)(x-1)?

Answer 1

Given the function:

`g(x)=(x+1)/((x+1)(x-1))`

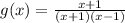
Let's find the domain of the function.

The domain is all set of x values which makes the function defined.

To find the domain, set the denominator to zero and solve for x.

We have:

(x + 1)(x - 1) = 0

Set the individual factors to zero and solve for x.

x + 1 = 0

Subtract 1 from both sides:

x + 1 - 1 = 0 - 1

x = -1

x - 1 = 0

Add 1 to both sides:

x - 1 + 1 = 0 + 1

x = 1

Therefore, the domain of the function in interval notation is:

`\mleft(-\infty,-1\mright)\cup(-1,1)\cup(1,\infty)`

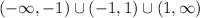
ANSWER:

`\mleft(-\infty,-1\mright)\cup(-1,1)\cup(1,\infty)`