Given:
The two forces are:
F1= <-2 , -7>
F2=< 3 , 1>
The angle between the two forces is given by the dot product of the two forces.
Thus,
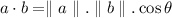
Where, a and b are the two forces and theta is the angle between them
Substituting the values in this formula,
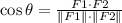
Now,
![\begin{gathered} \parallel F1\parallel=\sqrt[]{(-2)^2+(-7)^2} \\ =\sqrt[]{4+49} \\ =\sqrt[]{53} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/nhpfbwki5jaw6xo4bxi13tl29vycqpun47.png)
![\begin{gathered} \parallel F2\parallel=\sqrt[]{(3)^2+(1)^2} \\ =\sqrt[]{9+1} \\ =\sqrt[]{10} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/spzrf0x395r3jvjuyvf453qtdmev8zmxnn.png)
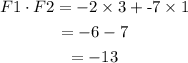
Hence, the angle between the forces is:
![\begin{gathered} \cos \theta=\frac{-13}{\sqrt[]{53}*\sqrt[]{10}} \\ =\frac{-13}{\sqrt[]{530}} \\ =(-13)/(23.021) \\ =-0.564 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/rolca9ptl6uv245nrhs5p2gqlmkhb7sxm1.png)
Now,solving further:
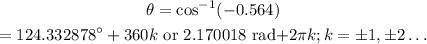
Hence, the angle between the forces is 124.332878 degrees or 2.170018 radians.