Question

The average number of mosquitos in a stagnant pond is 60 per square meter with a standard deviation of 16. If 25 square meters are chosen at random for a mosquito count, find the probability that the average of those counts is more than 62.9 mosquitos per square meter. Assume that the variable is normally distributed.

Answer 1

In this problem, we have a variable normally distributed X such that:

• X = average of mosquitos per square meter,

,

• the mean ,μ = 60 mosquitos/m²,,

,

• the standard deviation ,σ = 16 mosquitos/m²,.

We want to compute the probability that the average of mosquitos will be:

`P=P(X>X_1=62.9/m^2)\text{.}`

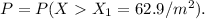
Now, we can rewrite this probability in the following way:

`P=P(X>X_1=62.9/m^2)=1-P(X\le X_1=62.9/m^2)\text{.}`

Because the variable is normally distributed, we can compute the probability using the z-scores:

`Z_1=(X_1-\mu)/(\sigma)=(62.9-60)/(16)=0.18.`

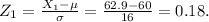
The probability in terms of the z-score is:

`P=1-P(Z\le Z_1=0.18)=1-0.5719=0.4281.`

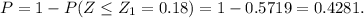
Where we have used a table to get the value of z-score probability P(Z ≤ 0.18).

Answer

The probability that the average of those counts is more than 62.9 mosquitos/m² is 0.4281.