ANSWER
C. The rate of heat transfer for both walls is the same
Step-by-step explanation
The rate of heat transfer for a material is given by:
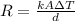
where k = thermal conductivity
A = surface area of the material
ΔT = change in temperature
d = thickness of the material
Wall A has 4 timesthe area of Wall B and is also twice as thicjk as wall B. This implies that:
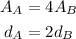
We also have that the thermal conductivity of Wall A is half that of Wall B:

Therefore, the rate of heat trnsfer for Wall ABis:
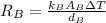
and for Wall A is:
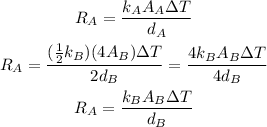
Note: ΔT is the same for both walls
Hence, we see that the rate ofheat rtransfer for both walls is the same.
The correct option is option C.