Question

If you are not knowledgeable in college algebra please let me know so I may move on more quickly. Thanks in advance!

Answer 1

The function we have is:

`f(x)=2x^6+4x^2+8`

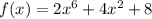
To find the zeros of a polynomial function, we are looking for the numbers that meet the condition:

`2x^6+4x^2+8=0`

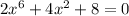
If we can't find any number or numbers that meet this condition, the function will not have any real solutions or zeros.

Let's analyze the equation:

`2x^6+4x^2+8=0`

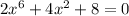
The first term is

`2x^6`

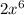
since the exponent of the x is an even number (6), x^6 will always be positive (unless the value of x is 0).

To demonstrate this point we can see some examples:

`\begin{gathered} (-2)^6=(-2)(-2)(-2)(-2)(-2)(-2)=+64 \\ (-1)^6=(-1)(-1)(-1)(-1)(-1)(-1)=+1 \\ (2)^6=(2)(2)(2)(2)(2)(2)=+1 \end{gathered}`

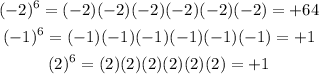
as we can see, the result is a positive number. So is x is not 0, x^6 will be positive.

The same happens with the second term: 4x^2, since the exponent of the x is an even number x^2 will be a positive number.

And the third term +8 is already a positive number.

Thus, the equation

`2x^6+4x^2+8=0`

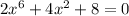
cannot have a solution in which the sum of the three terms is 0, because all of the terms are positive numbers and the result will be greater than 0.

The only other option we can discard is 0, because:

`2(0)^6+4(0)^2+8=0+0+8=8`

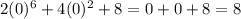
The result is 8 and not 0. So 0 cannot be the solution, nor any other real number.