The first step is to find the probability for each of the events, which are pick up a gold marble, pick up a silver marble and pick up a black marble:
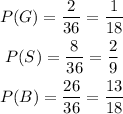
Now, multiply each of the probabilities by its corresponding reward and find the sum of them to find the expected value:
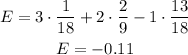
The expected value is -$0.11.