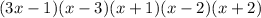Question

Factor the given polynomial:P(x) = 3x^5 - 7x^4 + 5x^3 - 25x^2 - 28x + 12. 2i is a zero.

Answer 1

`(3x-1)(x-3)(x+1)(x-2i)(x+2i)`

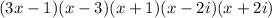
Step-by-step explanation

We want to factor the given polynomial:

`3x^5\:-\:7x^4\:+\:5x^3\:-\:25x^2\:-\:28x\:+\:12`

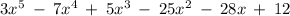
We have that 2i is a zero. This implies that the polynomial is divisible by (x - 2i).

If it is divisible by (x - 2i), then, it must be divisible by (x + 2i) and the product of the two factors must also be a factor:

`\begin{gathered} (x-2i)(x+2i) \\ \\ \Rightarrow x^2+4 \end{gathered}`

Let us now divide the polynomial:

Now, the polynomial has been reduced to:

`(3x^3-7x^2-7x+3)(x^2+4)`

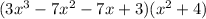
Let us reduce this further. To do this, we must find a term that is a factor of the polynomial in the first bracket.

Let us try to divide the polynomial by (x + 1):

Now, we have factorized the polynomial further:

`(3x^2-10x+3)(x+1)(x-2i)(x+2i)`

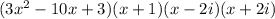
Now, let us factorize the quadratic expression:

`\begin{gathered} 3x^2-10x+3 \\ \\ (3x^2-9x-x+3) \\ \\ 3x(x-3)-1(x-3) \\ \\ (3x-1)(x-3) \end{gathered}`

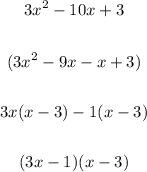
Therefore, the factored polynomial is:

`(3x-1)(x-3)(x+1)(x-2\imaginaryI)(x+2\imaginaryI)`