The revenue generated by the drama club play on the first night is given as:

The production teams projects the revenue earned each successive day to be 70% of the previous day. Therefore, we expect a 30% cut in revenue generated in each successive day for next five days.
Using the above information we can forecast the revenue to be generated in next 5 days as follows:

We can write the revenue for 6 days in a sequential form as follows:
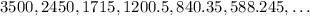
We see that the above sequence follows a geometric progression. Where the parameters of geometric progression are as such:
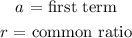
Where for this sequence the constant parameters are:
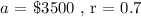
The revenue earned ( Rn ) at the nth day till 5 days can be modeled by using geomtric progression nth terms formula as such:
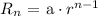
By plugging in the respective constants ( a and r ) we can get the function rule that models the given situation as such:
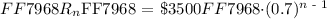
Where, n = The nth consecutive day of the working week!